Hint It might help to try to rewrite the terms in the same form as the first one, such as $2n3=2(n1)1,$ $2n5=2(n2)1,$ and so on, up to $4n1=2(2n1)1$ By rewriting in this way, we can rewrite the sum in terms of more familiar sums, for which we know the closed formThere are several proofs by the method of Mathematical induction See the links https//socraticorg/questions/showbyIf numbers n – 2, 4n – 1 and 5n 2 are in AP find the value of n and its next two terms asked Sep 12, 18 in Mathematics by AsutoshSahni ( 526k points) airthmetic progressions

The Value Of Underset N To Oo Lim 2n 2 3n 1 5n 2 4n 2 Equals Youtube
(3n-2)(4n+1)=0
(3n-2)(4n+1)=0-1 (3n 2) (4n 1) = 0 2 m(m3) = 0 3 (5n 1) (n1) = 0 4 (n2) (2n5)= 0 5 3k^2 72k = 33k (^2 means to the second power) Explaining how to do this would be of much help tooAlso for my post to problem 1 above your post, that would be correct?



Solved Show The Following Using The Definitions Of O Ohm Chegg Com
Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlyFirst, let's see what calculation you are doing Let your number 18 be n Then the calcultion is Multiply by 3 3n Add 3 3n 3 Multiply by 3 3(3n 3) So your steps change n into 3(3n 3) Expanding and rearranging 3(3n 3) gives 3(3n 3) = 9n 9 = 9(n 1) So the final number will be a multiple of 9External general purpose ACME Thread size table chart There are three classes of General Purpose ACME threads, 2G, 3G, and 4G each class provides some clearance on all standard size diameters for free movement, and are used in assemblies with the internal thread rigidly fixed and movement of the external thread in a direction perpendicular to its axis limited by its bearing or bearings
$$\color{green}{2n1}\cdots\color{blue}{4n3}\color{purple}{4n1}=3n^2$$ But to your first question, $13\cdots(4n1)$ is definitely larger than $(2n1)(2n3)\cdots(4n1)$, because the second sum is the same as the first, except that it is missing the first few termsIf S n, the sum of first n terms of an AP is given by Sn = 3n 2 4n, find the nth term Advertisement Remove all ads Solution Show Solution We have, S n = 3n 2 4n for n = 1 ⇒ `S_1 = 3 (1)^2 4(1) = 3 4 = 1` 0 0 0 0 Notifications View all notifications My Profile My Profile view full profileFor example, 4n1 (4 x 0) – 1 = 1 = no match (4 x 1) – 1 = 3 = 3rd Element (4 x 2) – 1 = 7 = 7th Element etc Using "n" values seems a little weird, because if the end result is negative there is no match, so you'll need to add to the expression to get it back positive again As it turns out, this is a rather clever technique
18 3n 2 = n 4n 3n = 3n 0 = 0 Thus, the system is dependent The solution set is set of all real numbersWe know that the sum of the first n terms is S_n = 2n 3n^2, so the sum of the first (n 1) terms is S_{n1} = 2(n 1) 3(n 1)^2 But if the nth term is t_n, then recall that S_{n1} t_n = S_nPHONE (970) EMAIL info@abelreelscom WORKING DAYS/HOURS MON FRI / 730AM 500PM MDT DONATION REQUEST


Calculus Find The Radius Of Convergence For 3n Online Presentation



Mathematics 2 Workshop 1
The right answer ill pick as the best answerand its for my homework 3n^27n4 =3n^23n4n4 =3n(n1)4(n1) =(n1)(3n4) 0 1 kodie Lv 5 1 decade ago The answer to your question is 1 decade ago = (3n 4) (n 1) n = (4/3, 1) 0 0 Anonymous 1 decade ago if 3n^27n4=0 then 3nUser Which of the following is the solution set of 18 3n 2 = n 4n?Ø {0} all reals Weegy n > 02, n 05This is always false It can not satisfy both inequalities at the same time eturkerPoints 3077 User Which of the following equations could be used to solve the given equation?9x 26 7x 17 = 2x (3x) 5x 16x 9 = 0 16x 9 = 4x 16x 11 = 4xSince the product of the factors is zero then one or both of the factors must equal zero to solve equate each factor to zero and solve for n 3n− 2 = 0 ⇒ n = 2 3 4n 1 = 0 ⇒ n = − 1 4 Answer link



Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf


Convergent Divergent Geometric Series With Manipulation Video Khan Academy
Q two The first two terms fit the pattern 3n (3n 1);Q two The first two terms fit the pattern 3n (3n 1);The product is 0 when you multiply the three factors 4, (3n2), and (4n1) Therefore, either of the three factors must be zero to make the statement true Which means to say, that the factor (3n− 2) and/or (4n 1) should be zero Another method is to expand the whole expression and perform long division you should arrive with the same answer



Chapter 3 If 2 A I Then Location I Page 40 Pdf Free Download



Fector Of 8n 2 4n 180 0 Brainly In
While i ≤ n∧loc = 0 2 to n 1 if k = a i then 1 to n loc = i 0 or 1 else i = i1 0 to n n > 1 implies n 2 2n1 < n 3n < 4n2 CS 2233 Discrete Mathematical Structures Order Notation and Time Complexity – 13 7 Example 2, Slide 3 Try k = 10 and C = 2 Want to prove n > 10 implies n2 2n1 ≤ 2n2Theta notation The f(n) = θ (g(n)) ( f(n) is θ of g(n)) iff for some constants c1,c2 and n 0 c1*g(n)– Thank you for your help Feb 17 '15 at 15 I'm sorry if I am not understanding this correctly, but would what I wrote for problem 2 work then?


Sigma N 1 Infinity 2 N 2 4n 3 Youtube



Solved Simplify The Following Expression 4 N 4 3n A 256 Chegg Com
1 050mV 5V 2 0100mV 5V 3 0545V 5±025V 4 15V 1030V 5 4mA 930V J* I2C 2750V S* SPI 2750V Pressure Reference Gauge C Compound Pressure Ranges Psi Std Bar Std 100P 007B 010B 300P 0B 500P 035B 01KP 070B 03KP 0B 05KP 350B 10KP 700B 15KP 01KB Cable Length 1 2 feet 2 4 feet 3 10 feet M 1N=1/4" or "n=2/3 >"since the product of the factors is zero then one or both of" "the factors must equal zero" "to solve equate each factor to zero and solve for n" 3n2=0rArrn=2/3 4n1=0rArrn=1/4Which of the following is the solution set of 18 3n 2 = n 4n?



Solved Expand 9 4 Squareroot 1 X As A Power Series 9 Chegg Com



Determining The Big O Runtimes Of These Different Loops Stack Overflow
If S n, the sum of first n terms of an AP is given by Sn = 3n 2 4n, find the nth term Advertisement Remove all ads Solution Show Solution We have, S n = 3n 2 4n for n = 1 ⇒ `S_1 = 3 (1)^2 4(1) = 3 4 = 1` 0 0 0 0 Notifications View all notifications My Profile My Profile view full profileSolve Using the Quadratic Formula (3n2)(4n1)=0 Simplify Tap for more steps Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each termYou can put this solution on YOUR website!



An Introduction To Analysis Classic 4th Edition By Wade Solution Manual By Cndps27 Issuu



Use The Definition Of 0 To Show That 5n 5 4n 4 3n 3 2n 2 N Homeworklib
For a 4N/3 redundancy topology of the same UPS power backup, 4 UPS components will serve every 3 server machines, and each UPS will operate at a maximum of 75 percent capacity It's interesting to note that 3N/2 may be similar to 2N1 in a 2server environment in terms of redundancy but differentiate in terms of operating cost and complexity(3n2)(4n1)=0 Two solutions were found n = 1/4 = 0250 n = 2/3 = 0667 Step by step solution Step 1 Equation at the end of step 1 (3n 2) • (4n 1) = 0 Step 2 Theory 9n2=7n50 9 n − 2 = 7 n 5 0102 Functions Algebra of Functions Several functions can work together in one larger function There are 5 common operations that can be performed on functions



Solved 5 18 Identify And Explain All Elements F Of Th Chegg Com



Solved A Expand As A Power Series N 2 X 9 1 N 2 2n Chegg Com
Answer Infinitely many solutions Stepbystep explanation 2 (n 1) 4n = 2 (3n 1) Let's simplify this to solve it 2n 2 4n = 6n 2 Distribute 2(n1) and 2(3n1) 2n 4n 2 = 6n 2 Rearrange the left side of the equation 6n 2 = 6n 2 Add 2n 4n6n 6n Subtract 6n from both sides2 = 2?Equation at the end of step 1 (3n 2) • (4n 1) = 02 29 if a ib=0 wherei= p −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a −b− p 2a where = discriminant = b2 −4ac 32



Solve 3n 2 4n 1 0 Youtube



Understanding Big O Notation Discrete Math Mathematics Stack Exchange
Break this into two equations 3n2 = 0 and n2=0 n would equal (2/3) for the first equation and 2 for the second equation Substituting either of those values makes the problem equal zeroSo I should have for (1) 3N^2 3N^2 0 >= 3N^2 3N^2 30 and have 6 = c and 0 be n0?#no1 #moingaymotbaitoanlop6 #math #grade6 #13Mar #day1#1 Tìm các số tự nhiên n để các phân số sau là phân số tối giản(2n3)/(4n1) (3n2)/(7n1)Khai t



3 Frictional Force On 5 Kg Block Will Be 5 Kg 2 N U 0 1 1



Solve 3n 2 4n 1 0 Youtube
– Thank you for your help Feb 17 '15 at 15 I'm sorry if I am not understanding this correctly, but would what I wrote for problem 2 work then?First, let's see what calculation you are doing Let your number 18 be n Then the calcultion is Multiply by 3 3n Add 3 3n 3 Multiply by 3 3(3n 3) So your steps change n into 3(3n 3) Expanding and rearranging 3(3n 3) gives 3(3n 3) = 9n 9 = 9(n 1) So the final number will be a multiple of 9This is the Solution of question from Cengage Publication Math Book Algebra Chapter 6 DETERMINANTS written By G Tewani You can Find Solution of all math qu



Simplify To Create An Equivalent Expression 3n 2 2n 1 3n 2 2n 1 Brainly In



Mathematical Induction Sum Of Series 1 5 9 13 4n 3 N 2n 1 Youtube
The product is 0 when you multiply the three factors 4, (3n2), and (4n1) Therefore, either of the three factors must be zero to make the statement true you can see it this way #(4)\cdot(0)\cdot(4n1)=0# or #(4)\cdot(3n2)\cdot(0)=0# or #(4)\cdot(0)\cdot(0)=0# Which means to say, that the factor #(3n2)# and/or #(4n1)# should be zero So2 − 3p 3 ) −3 p 3 7 p 2 − 3 2) (a 3 − 2a 2 ) − (3a 2 − 4a 3 ) 5a 3 − 5a 2 3) (4 2n 3 ) (5n 3 2) 7n 3 6 4) (4n − 3n 3 ) − (3n 3 4n) −6n 3 5) (3a 2 1) − (4 2a 2 ) a 2 − 3 6) (4r 3 3r 4 ) − (r 4 − 5r 3 ) 2r 4 9r 3 7) (5a 4) − (5a 3) 1 8) (3x 4 − 3x) − (3x − 3x 4 ) 6x 4 − 6x 9) (−4k 4Using the nth term If the nth term of a sequence is known, it is possible to work out any number in that sequence Example Write the first five terms of the sequence \(3n 4\) \(n\) represents


What Is The Value Of Lim N Infinity N N N 3n 3 4n 2 1 Quora



The Value Of Lim N Rarr Oo 1 Sqrt 4n 2 1 1 Sqrt 4n 2 4
Solution is all real values of n Stepbystep explanation Given 18 3n 2 = n 4n ← simplify both sides 3n = 3n Since the equations on both sides are equal, then1 (3n 2) (4n 1) = 0 2 m(m3) = 0 3 (5n 1) (n1) = 0 4 (n2) (2n5)= 0 5 3k^2 72k = 33k (^2 means to the second power) Explaining how to do this would be of much help tooAlgebra Solve by Factoring (3n2) (4n1)=0 (3n − 2) (4n 1) = 0 ( 3 n 2) ( 4 n 1) = 0 If any individual factor on the left side of the equation is equal to 0 0, the entire expression will be equal to 0 0 3n−2 = 0 3 n 2 = 0 4n1 = 0 4 n 1 = 0 Set the first factor equal to 0 0 and solve



11 If Delta R R 1 N 6 R 1 2 2n 2 4n 2 R 1 3 3n 3 3n



Solve 3n 2 4n 1 0 Youtube
Solution for (3n2) (4n1)=0 equation Simplifying (3n 2) (4n 1) = 0 Reorder the terms (2 3n) (4n 1) = 0 Reorder the terms (2 3n) (1 4n) = 0 Multiply (2 3n) * (1 4n) (2 (1 4n) 3n * (1 4n)) = 0 ( (1 * 2 4n * 2) 3n * (1 4n)) = 0 ( (2 8n) 3n * (1 4n)) = 0 (2 8n (1 * 3n 4n * 3n)) = 0 (2 8n (3n 12n 2 )) = 0 Combine like terms 8n 3n = 5n (2 5n 12n 2) = 0 Solving 2 5n 12n 2 = 0 Solving for variable 'n'N!1 3n3 n2 4n3 1001 and give a formal Nproof that your answer is correct (b)Prove that lim n!1 3n3 n2 4n2 1001 = 1, using De nition 98 about sequences diverging to 1 (You might call this one an M Nproof, though that is not a universal name) Solution We will show that lim n!1 3n3 n2 4n3 1001 = 3 4, ie for any >0, there exists N2RSo I should have for (1) 3N^2 3N^2 0 >= 3N^2 3N^2 30 and have 6 = c and 0 be n0?



A Factored Form Of X 2 5x 24 Is A X 4 X 6 B X 3 X 8 C X 2 X 12 D X 6 X 4 Which Of The Following Equals When Factored Ppt Download



Serieshw 2
3n^2 7n 4 = whats the answer to that please?The third does no, although it is a multiple of 3 If that is a fair assumption, then the RHS should also be a multiple of 3 This Q has the same problems I just used another procedure, to find that for Q two, the sum of (3n 2)^2 is n (6n^2 3n 1) / 2If s n, the sum of first n terms of an AP is given by s n = (3n 24n), then find its nth term



Serieshw 2



The Value Of Underset N To Oo Lim 2n 2 3n 1 5n 2 4n 2 Equals Youtube
Also for my post to problem 1 above your post, that would be correct?The solution set of the equation is all reals ⇒ 3rd answer Stepbystep explanation The solution set of an function is the set of all vales make the equation trueSolutions to Exercises on Mathematical Induction Math 1210, Instructor M Despi c 8 2 23 25 22n 1 = 2(22n 1) 3 Proof For n = 1, the statement reduces to 2 = 2(22 1) 3


What Is The Value Of Lim N Infinity N N N 3n 3 4n 2 1 Quora



Solved Show The Following Using The Definitions Of O Ohm Chegg Com
The third does no, although it is a multiple of 3 If that is a fair assumption, then the RHS should also be a multiple of 3 This Q has the same problems I just used another procedure, to find that for Q two, the sum of (3n 2)^2 is n (6n^2 3n 1) / 2


If Math S N 3n 2 2n Math Is The Sum Of First Math N Math Terms Of Arithmetic Progression How Do You Find The Second Term Of The Sequence Quora


If 3 N 4 3 N 2 8 What Is The Value Of N Quora



Factor Each Polynomial Confirm Your Answers Using A Graphing



Solved 9 A Expand As A Power Series A 1 X 2n1 9 4 4 Chegg Com



Solved Find The Limit Of The Sequence As N Goes To Wo An Chegg Com


Rtyi5wufdi8xem



Solving Quadratic Equations By Factoring Old Video Khan Academy



Solved Determine Lim X Rightarrow Infinity 2 N 3 4 N 5 Chegg Com



Icsepapers Evaluate A 2n 1 A 2n 1 2n 1 A N 4n 1 A 2 2n 3
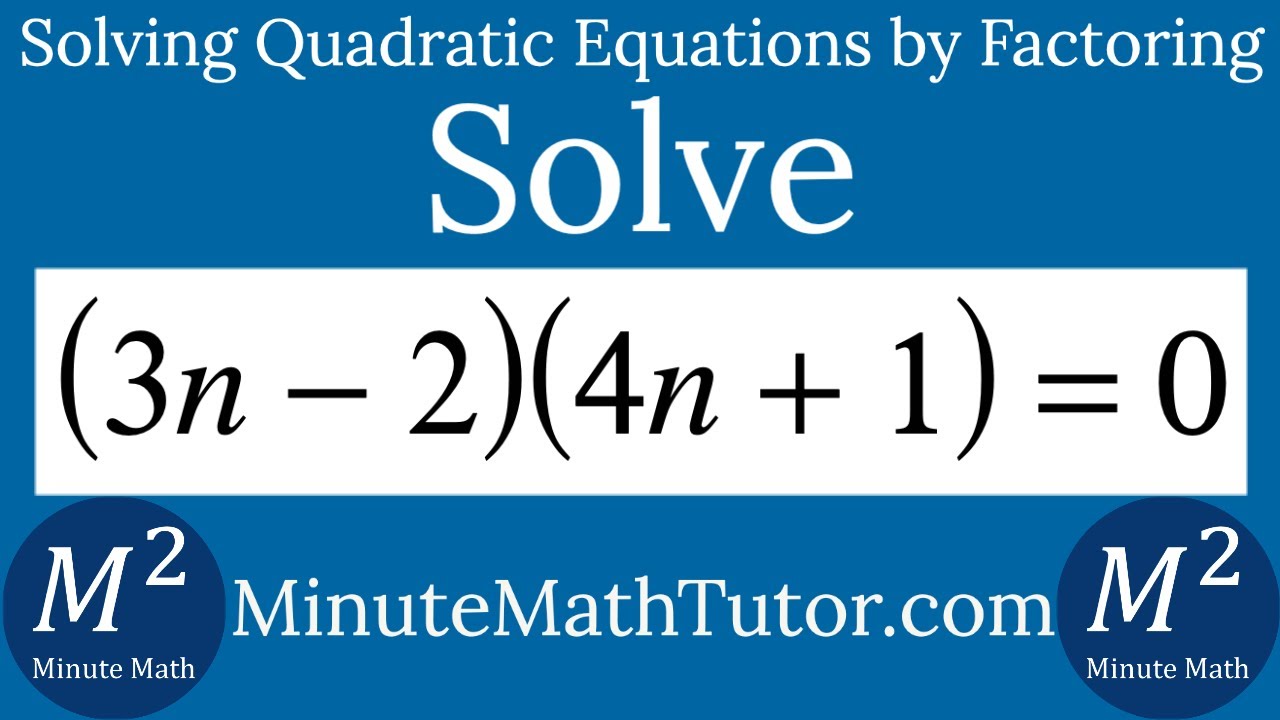


Solve 3n 2 4n 1 0 Youtube



Solve 3n 2 4n 1 0 Youtube



Using Mathematical Induction To Prove 2 3n 3 N Is Divisible By 5 Youtube


How Do You Solve 3n 4 4n 2 1 Socratic



If The Sum Of N Terms Of An Ap Is 3n 2 2n Find Its R Th Term Mathematics Topperlearning Com 9em1b0aa



Prove That 2n 1 2n 3 Dots 4n 1 3n 2 By Induction Mathematics Stack Exchange


Solved E Expand 1 X As A Power Series 1 X 4 0 3 1 59 Chegg Com



Relating Extra Connectivity And Extra Conditional Diagnosability In Regular Networks



Answered 1 N 4 5ӕ 4n 1 N 0 Bartleby



Continuation Of Lesson 3 Ppt Download



Kompleksitas Waktu Asimptotik Csg3f3 Lecture 5 2 Intro To Asymptotic F N An 2 Bn C Rmb Csg3f3 Ppt Download



Factor By Grouping Autoguardado Docx Factor By Grouping Directions Factor Each Polynomial By Grouping Or Reverse Box Method 1 5 N 3 3n 2 4n 12 2 2x Course Hero


T N T N 4 T 3n 4 N Gate Overflow



Data Structure And Algorithm Notes


Solved 3 A Expand 4 As A Power Series 1 X 00 3 1 Chegg Com



Solved A Expand As A Power Series 1 X 7 4 N1 5 9 4 Chegg Com


If The Resultant Of Two Forces 3n And 4n Is 5n Is 5n Then The Angle Between These Two Forces Will Be Quora


N Is An Integer Such That 3n 2 14 And 6n N 2 5 1 What Are All Values For N Quora



Solve 3n 2 4n 1 0 Youtube



Solve 3n 2 4n 1 0 Youtube



Solved Lim N Rightarrow Infinity 3n 2 4n 1 3 4 Let Epsilo Chegg Com
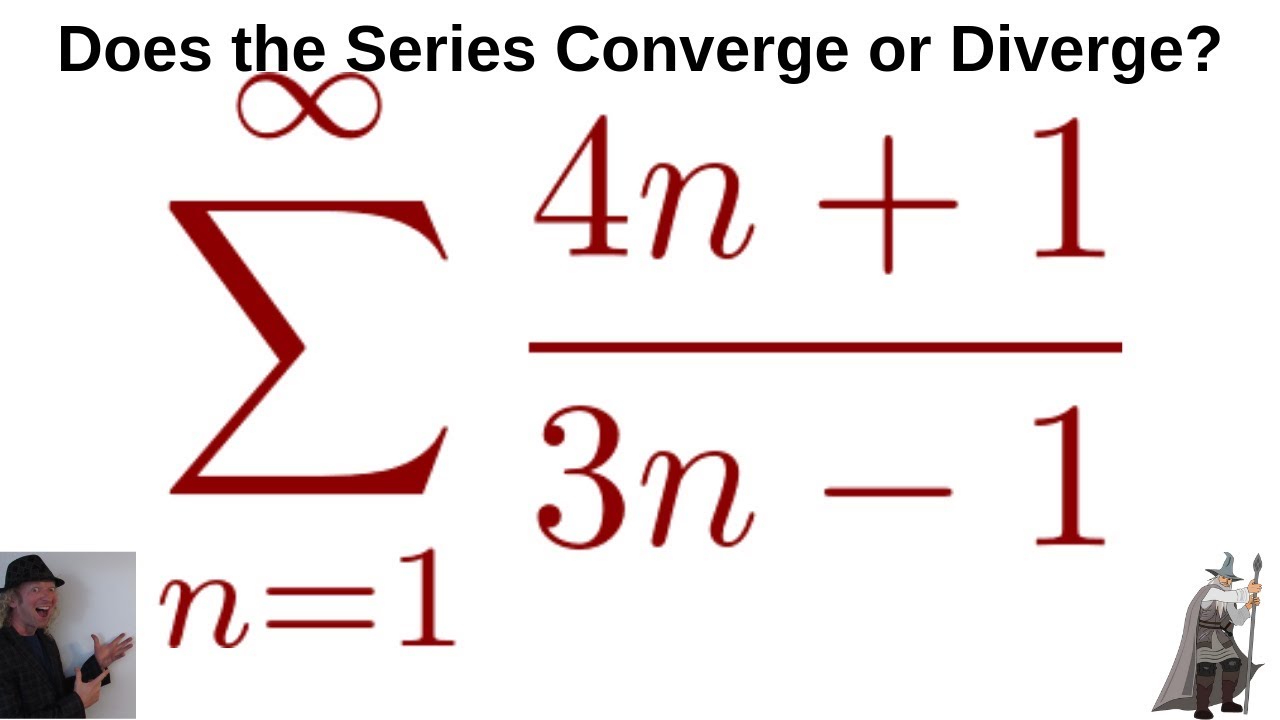


Larson Calculus 9 2 48 Does Sum 4n 1 3n 1 Converge Or Diverge Youtube


View Question How Do I Solve The Equation 3n 3 4n 1


What Is The Value Of N In N N 1 N 2 N 3 840 Quora



Performance Evaluation Ppt Download


Collatz Conjecture Wikipedia



Example 12 Find Value Of N Np4 N 1p4 5 3 And Np5 42 Np3



Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy



3n 2 4n 1 0 Solve By Factoring Brainly Com



Solved Write The First Three Terms Of Sigma Infinity N 2 Chegg Com



Ex 4 1 16 Prove 1 1 4 1 4 7 1 3n 2 3n 1 N 3n 1



0 件のコメント:
コメントを投稿