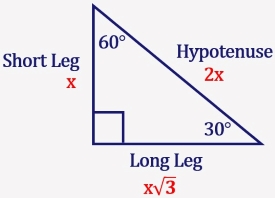
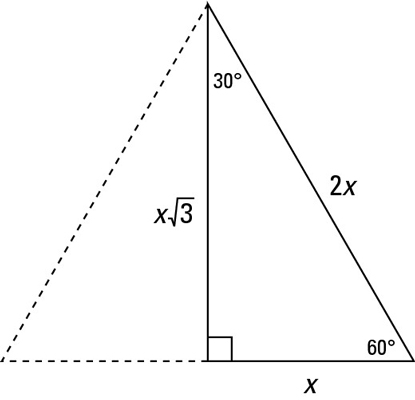
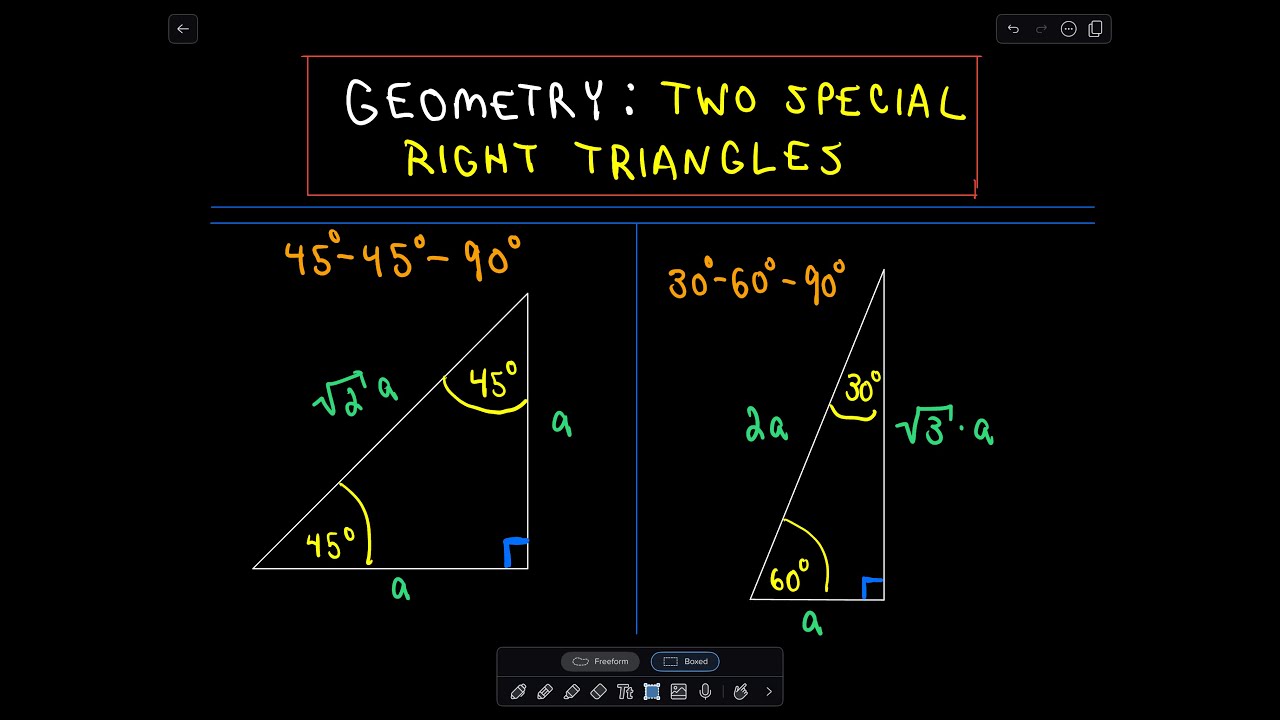
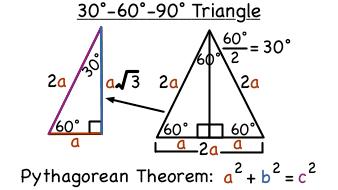
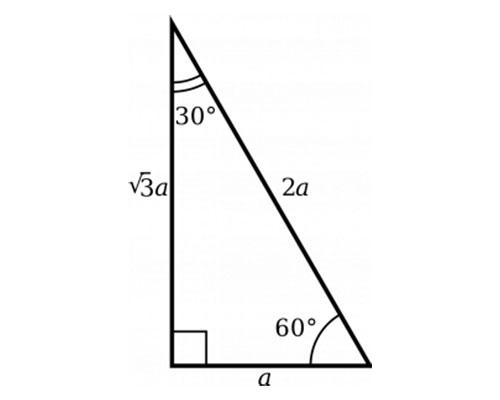
A right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads) The sides of a right triangle lie in the ratio 1√3230°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 x A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another The basic triangle ratio is
Special Right Triangle 30 60 90 Mathondemand Com
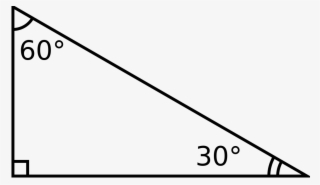
90 30 and 60 degree triangle
90 30 and 60 degree triangle-Answer (1 of 3) A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a triangleMore Buying Choices $3531 (7 used & new offers) Pack of 2 Large Transparent Metric Triangle Ruler Set Square 30 cm (12 Inch) 30/60 Degree & 22 cm (9 inch) 45/90 Degree Essential for School and Work use (cm Scale) 44 out of 5 stars




30 60 90 Triangle Theorem Ratio Formula Video
In A 30 60 90 Triangle The Shorter Leg Has Length Of 1 Minute Math 30 60 90 Triangles Youtube 30 60 90 Triangle Therom Slidedocnow 30 60 90 Triangle Therom Slidedocnow Does Sin Have A Value Quora Isee Math Review Triangle Types And Rules Piqosity 30 60 90 Triangles Geometry Lessons Math LessonsExample of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units inThe property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5
The triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 Here, a right triangle means being any triangle that contains a 90° angle A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90° 30°60°90° triangle is actually the equilateral triangle cut along the altitude The relationship between sides can be established by choosing hypotenuse as 2a The short leg (a) is opposite to 30° angle and it is half the length of the hypotenuse The30 60 90 Right Triangle Calculator Short Side a Input one number of input area Long Side b Hypotenuse c Area Perimeter Input one number then click "calculate" button!
A theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class roomCheck out this tutorial to learn about triangles!Answers 2 Get Other questions on the subject Mathematics Mathematics, 1800, RoyalGurl01 Identify which functions are linear or nonlinear a f(x) = x2 1 b f(x) = 2x 5 c f(x) = x 2 3 d f(x) = 3 x 7 e f(x) = 4x 10 2 5



1




30 60 90 Triangle Theorem Ratio Formula Video
The 30 – 60 – 90 degree triangle is in the shape of half an equilateral triangle, cut straight down the middle along its altitude It has angles of 30°, 60°, and 90° and sides in the ratio of The following figure shows an example Get acquainted with this triangle by doing a couple of problemsWhich triangle is a 30 60 90 degree triangle?How To Construct A 30 Degree Angle A 30 ° angle is half of a 60 ° angle So, to draw a 30 °, construct a 60 ° angle and then bisect it First, follow the steps above to construct your 60 ° angle Bisect the 60 ° angle with your drawing compass, like this Without changing the compass, relocate the needle arm to one of the points on the rays



45 45 90 And 30 60 90 Triangles Zona Land Education




Amazon Com C Thru Kt 80 Student 30 60 90 Triangle 9 75 In Musical Instruments
Table 1 sight triangle applicability table 2 360 ft design speed oncoming vehicles distance (sd) to minimum sight 25 mph 30 mph 35 mph 40 mph 45 mph 50 mph 400 ft 55 mph 440 ft 60 mph 480 ft 3 ft 280 ft 240 ft 0 ft from edge of curb) (approx 16 ft 41 ft(bb) collector streets 28 ft(bb) local and of the median in this area noTriangle30 60 90 This printable triangle has angles of 30, 60, and 90 degrees at its vertices Please make sure to print at 100% or actual size so the rulers will stay true to sizeA triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another




Amazon Com Pacific Arc Drafting Triangle 10 Inch 30 60 90 Degrees Topaz Office Products




10 30 60 90 Triangle
A triangle is a specific type of right triangle that has angles of 30 and 60 degrees in addition to the 90degree angle of all right trianglesThe other triangle is named a triangle, where the angles in the triangle are 30 degrees, 60 degrees, and 90 degrees Common examples for the lengths of the sides are shown for each below The Triangle Here we check A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middle




30 60 90 Triangle Theorem Ratio Formula Video



Right Triangle Degrees 30 60 90 Clipart Etc
By 30, at least 60 percent of Texans ages 2534 will have a certificate or degree The first goal in the plan, the 60x30 Educated Population goal, aims to increase the percentage of 25 to 34yearolds in Texas who hold a certificate or degree The goal focuses on 25 to 34yearolds as an indicator of the economic future of the state and its The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SAT a/c = sin (30°) = 1/2 so c = 2a b/c = sin (60°) = √3/2 so b = c√3/2 = a√3 Also, if you know two sides of the triangle, you can find the third one from the Pythagorean theorem However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given




Pacific Arc Clear Acrylic 30 60 90 Degree Professional Drafting Tria Omnitopia Supply



30 60 90 Triangle Geometry
A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangleAs the name suggests, the three angles in the triangle are 30, 60, and 90 degrees As a result, the lengths of the sides in a have special relationships between them that allow you toCheck out this tutorial to learn about triangles!
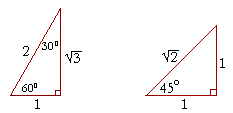



The 30 60 90 Triangle Topics In Trigonometry



Identifying The 30 60 90 Degree Triangle Dummies
This trigonometry video tutorial provides a basic introduction into triangles It explains how to evaluate trigonometric functions such as sine andA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and




A Quick Guide To The 30 60 90 Degree Triangle Dummies
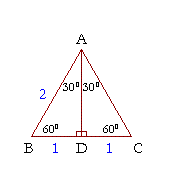



The 30 60 90 Triangle Topics In Trigonometry
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degreesBecause it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊ A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another



The Easy Guide To The 30 60 90 Triangle
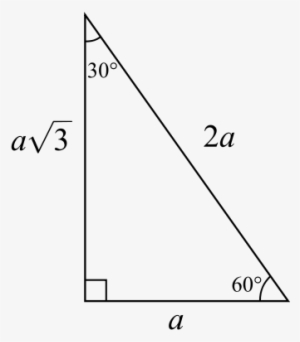



30 60 90 Triangle 30 60 90 Triangle Png Transparent Png 403x401 Free Download On Nicepng
This page shows to construct (draw) a 30 60 90 degree triangle with compass and straightedge or ruler We are given a line segment to start, which will become the hypotenuse of a right triangle It works by combining two other constructions A 30 degree angle, and a 60 degree angleBecause the interior angles of a triangle always add to 180 degrees, the third angle must be 90 degreesSpecial Right Triangles 30°60°90° triangle The 30°60°90° refers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of theThe hypotenuse is the longest side in a right triangle, which is different from the long leg The long leg is the leg opposite the 60degree angle Two of the most common right triangles are and the degree triangles All triangles




Triangle 4 30 60 Topaz Csu Bookstore



A 30 60 90 Triangle Math Central
Find the missing sides of the triangles ☐ triangle abc below is Hypotenuse = leg * v2 If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator for special right And Triangle Worksheet / Special Right Triangles 45 45 90 Degree And 30 60 90 Geogebra FindHere is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° anglesA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube



Aetxhkgd Svjxm
Large triangle ruler set come with a 6 inch 45/ 90 degrees triangle ruler and a 9 inch 30/ 60 degrees one Highquality material the set square is constructed of plastic material, durable and sturdy Translucent color allows for a clear view of numbers and letters on the pageThis allows us to find the ratio between each side of the triangle by using the Pythagorean theoremACCURATE INCH LENGTH The nongraduated triangle is an accurate inches long With 30, 60, and 90 degree corners, this triangle is one of the most versatile tools any profession should own Be able to make perfect angles for any project




30 60 90 Triangle Explanation Examples
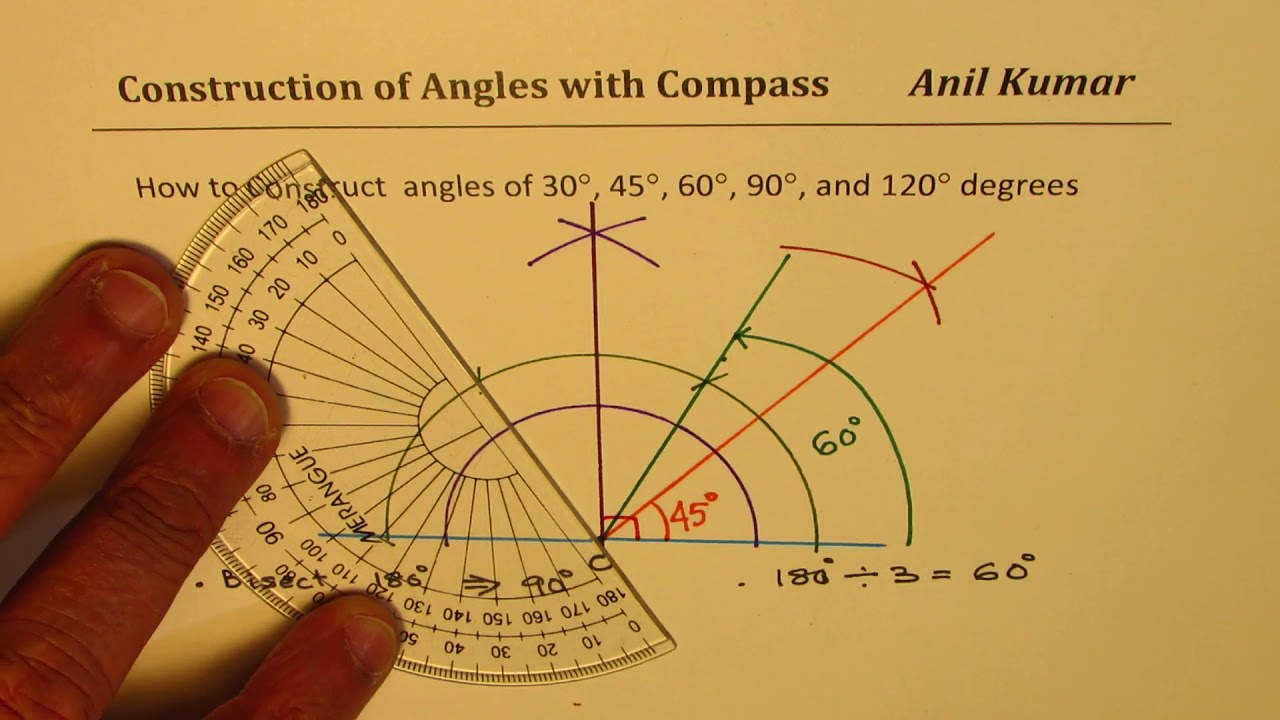



Construct Angles Of 30 45 60 90 1 Degrees With Compass Youtube
A triangle is a right triangle where the three interior angles measure 30° 30 °, 60° 60 °, and 90° 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides The 30 60 90 triangle is special because it forms an equilateral triangle when a mirror image of itself is drawn, meaning all sides are equal!To learn more about Triangles enrol in our full course now https//bitly/Triangles_DMIn this video, we will learn 000 triangle017 proof of 306



Solution If Triangle Abc Is A 30 Degree 60 Degree 90 Degree Triangle With M Anglea 30 Find Sin A Cos A And Tan A Give The Answers As Franctions With Simplified Radicals
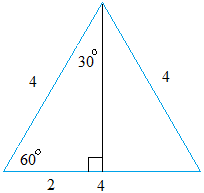



Using The 30 60 90 Triangle To Find Sine And Cosine
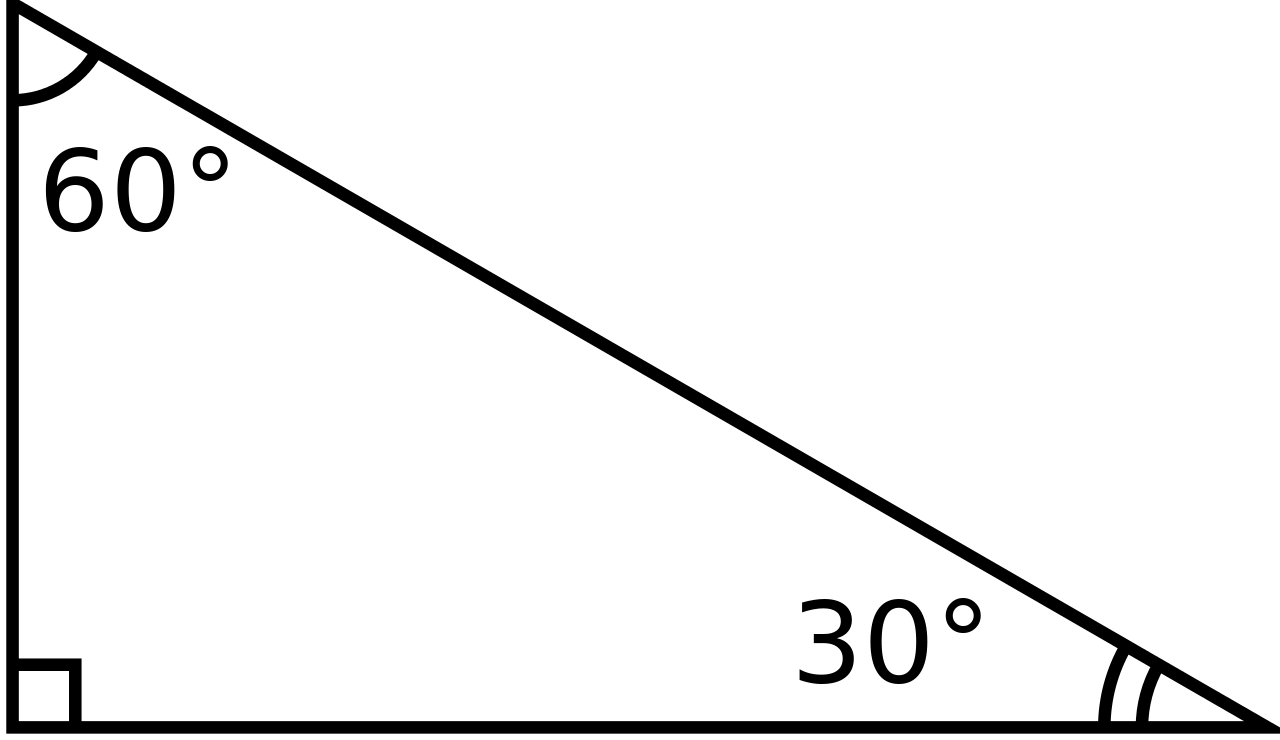



File 30 60 90 Triangle 2 Svg Wikimedia Commons
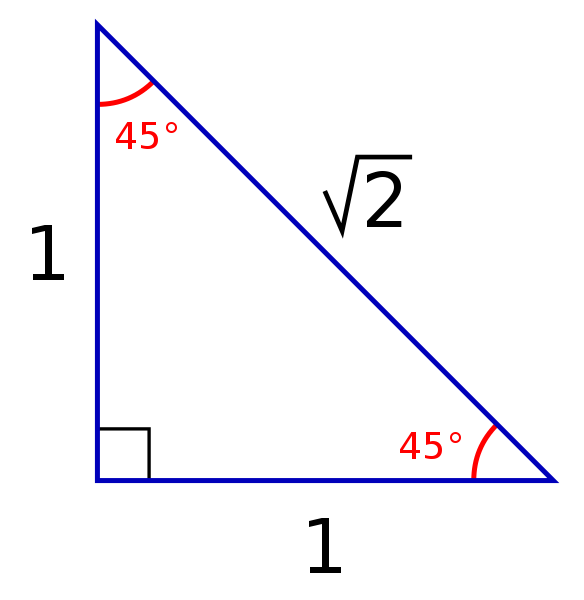



30 60 90 Triangle Formulas Rules And Sides Science Trends



The Easy Guide To The 30 60 90 Triangle




Special Right Triangle 30 60 90 Mathondemand Com
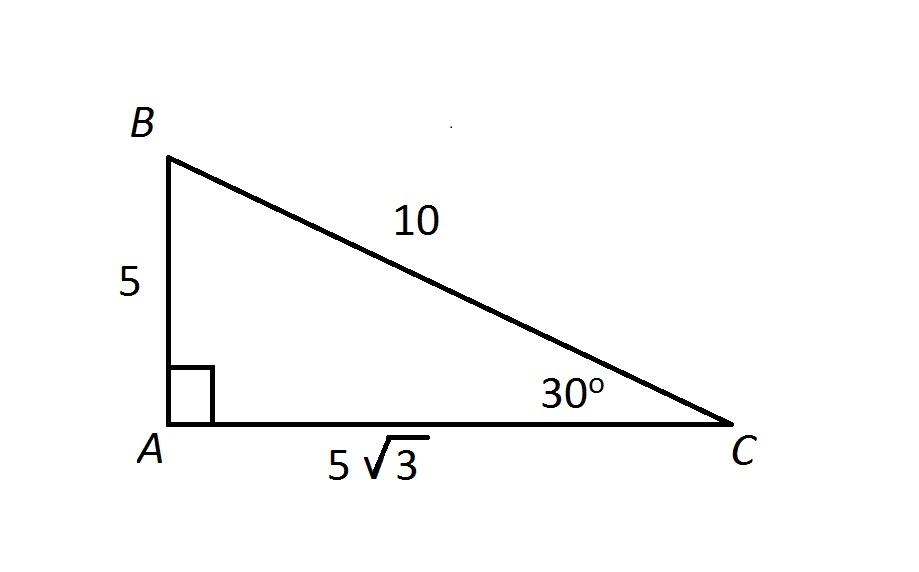



Special Triangles Hiset Math




Amazon Com Pacific Arc Drafting Triangle 14 Inch 30 60 90 Degrees Fluorescent Orange Office Products




Bronagrand Triangle Ruler Square Set 30 60 And 45 90 Degrees Set Of 2




Amazon Com Triangle Set 10 Inch 30 60 45 90 Office Products
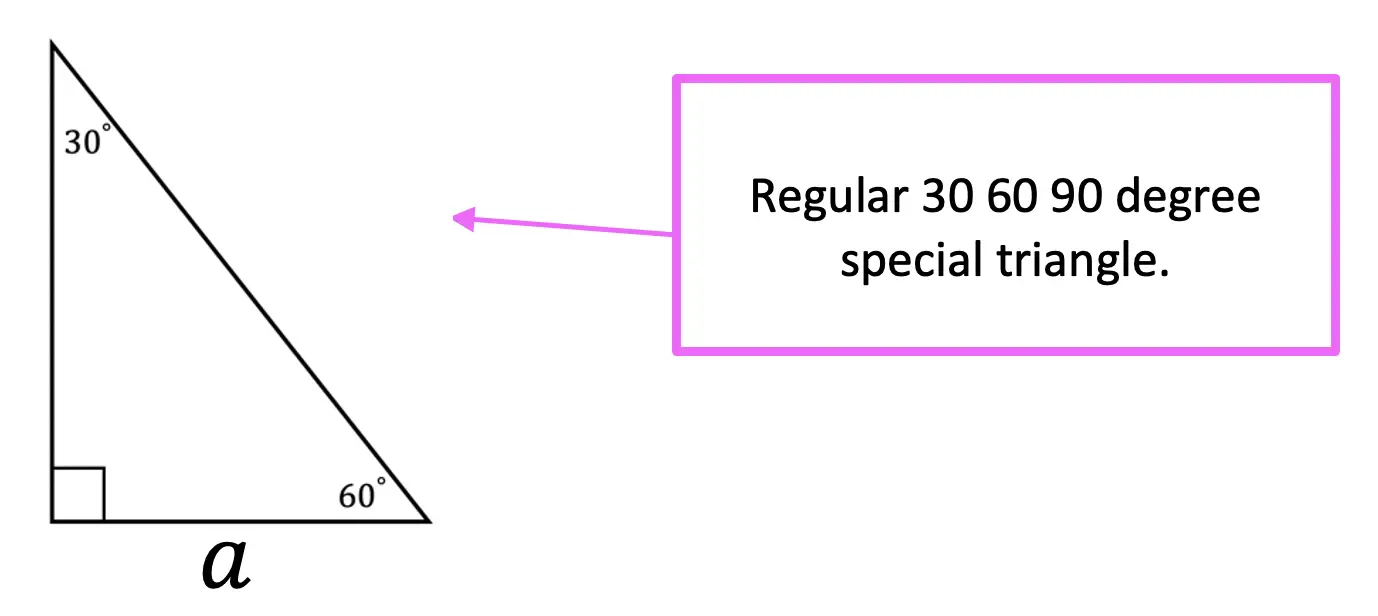



30 60 90 Special Triangles Geometry Mathsux 2




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies



If A Right Angled Triangle 30 60 90 Hypotenuse Is 10 Cm Then What Is The Length Of The Side Opposite To 60 Angle Quora




30 60 90 Triangles
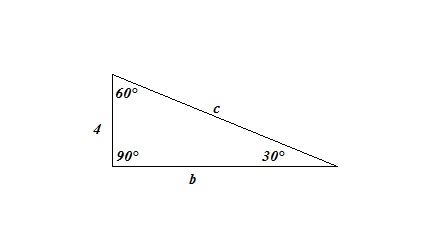



If You Have A Right Triangle 30 60 90 Degree Angles And You Have The Smallest Size Width To Be 4 How Do I Solve For X The Length Of The Triangle Socratic




The 30 60 90 Triangle Topics In Trigonometry



The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 12cm What Is The Length Of The Longer Leg What Is The Length Of The Shorter Leg Quora




30 60 90 Triangle Explanation Examples




The Complete Guide To The 30 60 90 Triangle




Which 30 60 90 Degree Triangle Is Labeled With The Correct Side Length Ratio Brainly Com




10 30 60 90 Degree Aluminum Triangle 5272 Alumicolor




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com




Special Angles 45 Degrees 30 60 Degrees 0 90 Degrees Trigonometry Youtube



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Definition Theorem Formula Examples
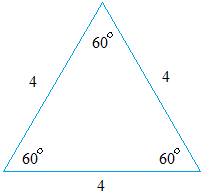



Using The 30 60 90 Triangle To Find Sine And Cosine




30 60 90 Triangle Theorem Ratio Formula Video



Right Triangles Gmat Free




30 60 90 Triangle Example Problem Video Khan Academy




30 60 90 Triangle Calculator Formula Rules




Unique Bargains Students 30 60 45 Degree Plastic Triangle Rulers Protractor Drawing Set 2 Pcs Walmart Com
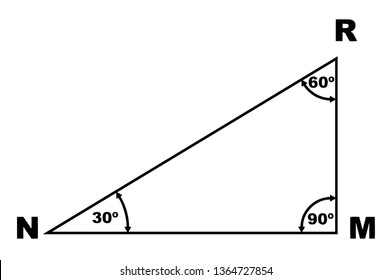



60 Degrees Triangle Images Stock Photos Vectors Shutterstock
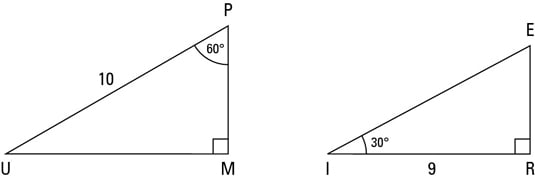



Identifying The 30 60 90 Degree Triangle Dummies




30 60 90 Right Triangle Side Ratios Expii




The Hypotenuse Of A 30 Degree 60 Degree 90 Degree Triangle Is 24 2 Ft Explain How To Find The Brainly Com



30 60 90 Triangle 30 Degree Right Angle Transparent Png 1024x592 Free Download On Nicepng



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube



1



The Easy Guide To The 30 60 90 Triangle




3 Ways To Find The Third Angle Of A Triangle Wikihow




30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Ratio Formula Video



What Is A 30 60 90 Degree Triangle Virtual Nerd Can Help




Triangle 30 60 90 Metric Printable Ruler



30 60 90 Triangle Sides Examples Angles Full Lesson




30 60 90 Triangle Definition Theorem Formula Examples



60 Degrees Triangle Images Stock Photos Vectors Shutterstock
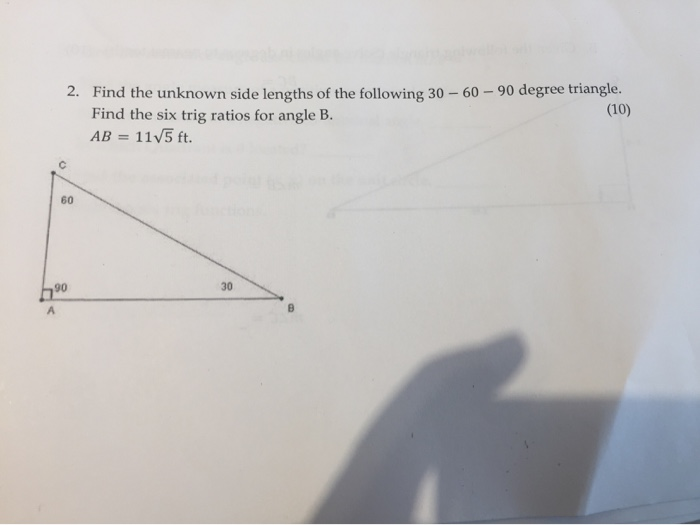



Solved 2 Find The Unknown Side Lengths Of The Following 30 Chegg Com
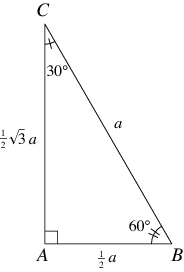



30 60 90 Triangle From Wolfram Mathworld




Amazon Com Coopay Large Triangle Ruler Set Square 30 60 And 45 90 Degrees Triangle Hollow Everything Else




Special Right Triangles Review Article Khan Academy



Right Triangles Gmat Free



Triangle Ruler Square Set 30 60 45 90 Degrees 27cm Triangle Rafter Angle Ruler 2 Pack Walmart Com



A 30 60 90 Triangle




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Explanation Examples



1




30 60 90 Triangle




Triangle Gma Is 30 Degree 60 Degree 90 Degree If M 26 Cm Find A And S Study Com
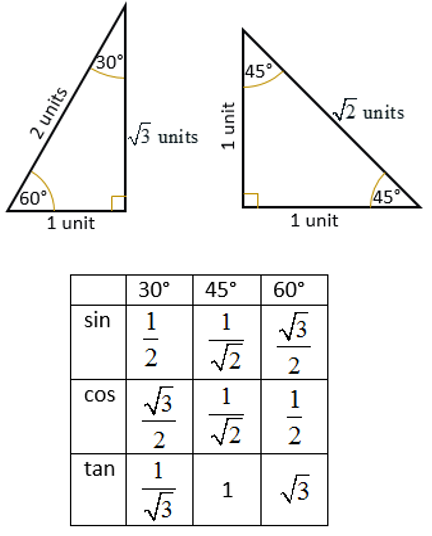



Trigonometric Ratios Of Special Angles 0 30 45 60 90 Video Lessons Examples And Solutions




A Triangle Has Three Angles 30 60 And 90 Degrees What Is The Value Of The Hypotenuse If The Long Leg Is 6 Feet Study Com



Construct A Triangle 30 60 90 Given The Hypotenuse Technical Graphics




30 60 90 Special Right Triangle Calculator Inch Calculator




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Calculator Formula Rules




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Triangle Classification By Angles Ck 12 Foundation




Set Square Blackboard 30 60 90 Degrees




The Complete Guide To The 30 60 90 Triangle




How To Construct A 30 60 90 Triangle With Compass And Straightedge Or Ruler Math Open Reference




30 60 90 Triangle Definition Theorem Formula Examples



The Easy Guide To The 30 60 90 Triangle
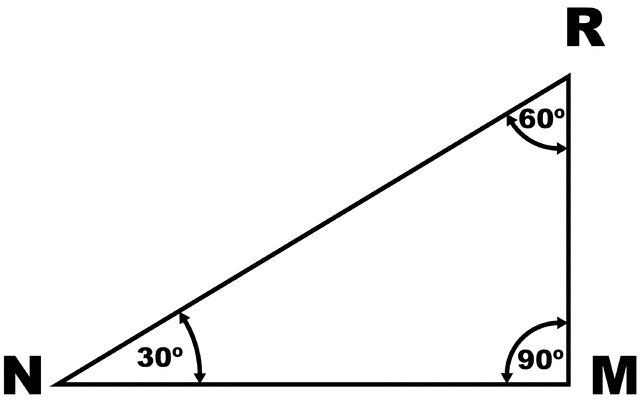



Triangle 30 60 90 Clipart Etc
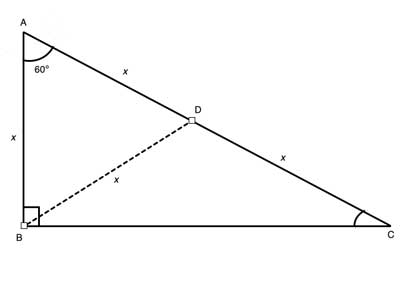



30 60 90 Triangle Geometry Help



1
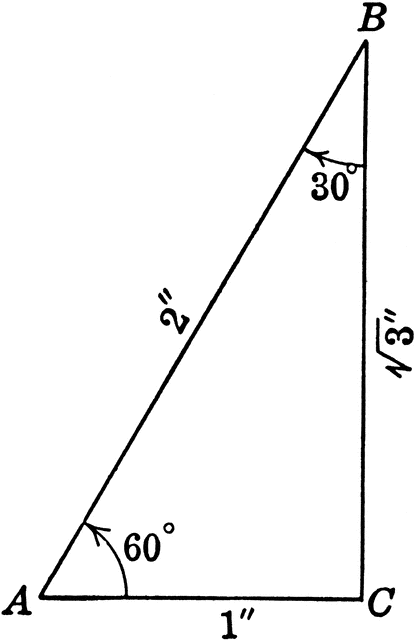



Special Right Triangle With Angles 30 60 90 Degrees Clipart Etc
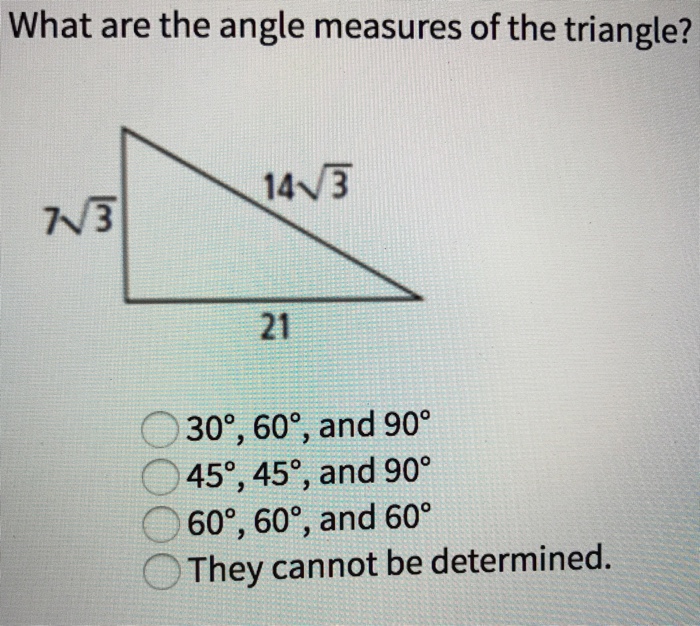



Solved What Are The Angle Measures Of The Triangle 30 Chegg Com



0 件のコメント:
コメントを投稿